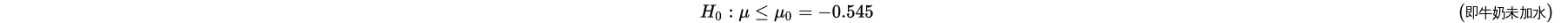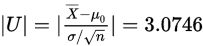5.1 一般总体数学期望的假设检验
经常是面对一个随机变量,其满足的分布不清楚,此时对总体的未知参数的假设检验属于非正态总体假设检验,即一般总体的假设检验问题。在样本很大(一般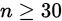 ,最好
,最好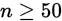 或
或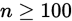 ),可以使用中心极限定理进行分析。
),可以使用中心极限定理进行分析。
5.1.1 一个总体均值的大样本假设检验
已知一个总体的均值和方差分别为: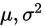 ,一个样本的均值和方差分别为:
,一个样本的均值和方差分别为: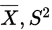 ,当n充分大时,由中心极限定理可知,
,当n充分大时,由中心极限定理可知,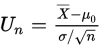 近似服从标准正态分布N(0,1)。所以这个问题可以使用U检验法进行分析。
近似服从标准正态分布N(0,1)。所以这个问题可以使用U检验法进行分析。
实际使用中,总体方差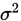 未知情况下,可使用样本方差
未知情况下,可使用样本方差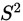 进行替代。
进行替代。
5.1.2 两个总体均值的大样本假设检验
两个总体的均值检验统计量可以构造如下:
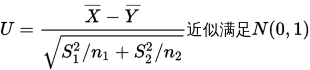
仍然使用U检验法进行检验。
5.2 假设检验问题的p值检验法
以上问题均属于临界值检验法,下面介绍P值检验法,所谓P值检验法就是由检验统计量的样本观察值得出的原假设可被拒绝的最小显著性水水平。
例子:
检验牛奶是否加水,牛奶冰点温度近似满足正态分布,加水会导致该冰点温度升高,其均值方差分别为-0.545和0.008,现抽样5批牛奶,得到均值为-0.534,问这批牛奶是否加水,取显著性水平为0.05.
首先提出假设:已知统计量观察值为:
P值<
,所以拒绝
,即认为牛奶加水了。
P值与显著性水平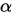 的关系
的关系
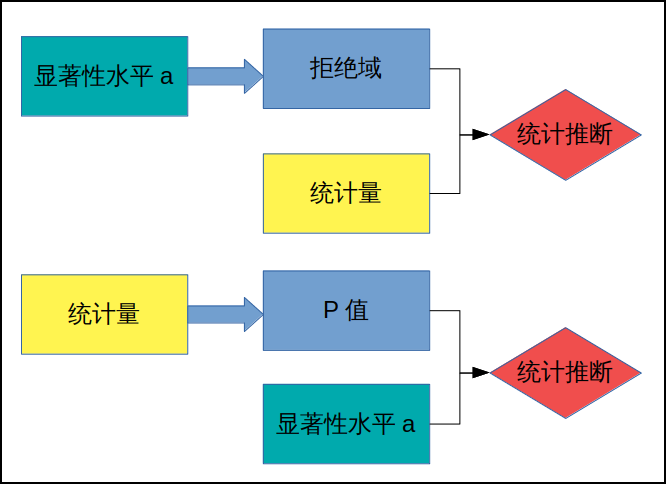
临界值法假设检验: 使用显著性水平得到统计量的拒绝域,结合样本统计量的值进行统计推断。
P值法假设检验: 由统计量得到P值,然后显著性水平进行比较得出统计推断。5.3 分布拟合检验
实际问题中,首先要根据样本的观察结果对总体的分布类型进行检验。使用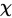 检验,可以检验总体是否具有某个指定的分布或者某个分布簇。
检验,可以检验总体是否具有某个指定的分布或者某个分布簇。
设总体的分布函数为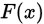 ,
,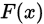 未知,
未知,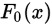 为某一已知分布函数,考虑如下检验问题:
为某一已知分布函数,考虑如下检验问题:
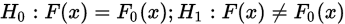
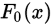 不含未知参数时,考虑如下:
不含未知参数时,考虑如下:
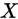 ,将其分为k段互不相交的区间,分点依次记为
,将其分为k段互不相交的区间,分点依次记为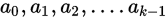 ,记
,记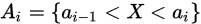 。
。 当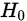 成立时,有:
成立时,有: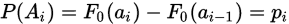 ,含义是随机变量落在区间
,含义是随机变量落在区间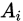 的概率。假设区间
的概率。假设区间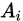 的长度是
的长度是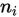 ,在n次的随机实验中,当
,在n次的随机实验中,当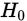 成立且n足够大时,
成立且n足够大时,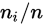 是
是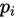 的近似。
的近似。
构造统计量1:用于衡量样本与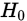 假设分布的吻合程度。
假设分布的吻合程度。
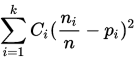
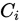 为给定常数,皮尔逊证明,当
为给定常数,皮尔逊证明,当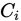 取
取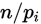 时,上面的式子可以变化如下:
时,上面的式子可以变化如下:
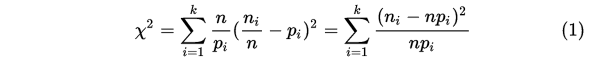
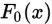 含有未知参数时,考虑如下:
含有未知参数时,考虑如下:
样本观察值,使用极大似然估计,求出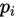 的估计值
的估计值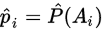 ,再使用上述公式(1)作统计量分析。
,再使用上述公式(1)作统计量分析。 皮尔逊定理:
- 若理论分布函数
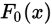 不含未知参数,则当
不含未知参数,则当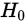 成立且n充分大是,统计量
成立且n充分大是,统计量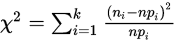 近似服从自由度为
近似服从自由度为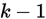 的
的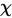 分布;
分布; - 若理论分布函数
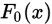 含有未知参数,其未知参数个数为r时,统计量
含有未知参数,其未知参数个数为r时,统计量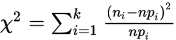 近似服从自由度为
近似服从自由度为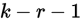 的
的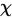 分布。
分布。
从公式来看,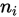 为区间i的实际频数,
为区间i的实际频数,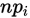 是理论频数。则统计量的含义可写为:
是理论频数。则统计量的含义可写为:

给定显著性水平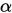 ,
,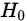 的否定域是
的否定域是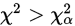
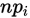 不能太小,一般是
不能太小,一般是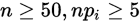 ,如果
,如果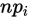 太小,可以进行合并。
太小,可以进行合并。 例子:
统计200天高速公路的车祸次数,得到下表信息| 车祸数i | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 频数n_i | 109 | 65 | 22 | 3 | 1 |
试问,在显著性水平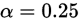 的情况下,是否认为X满足泊松分布。
的情况下,是否认为X满足泊松分布。
 ,根据样本观察结合极大似然估计得到:
,根据样本观察结合极大似然估计得到: 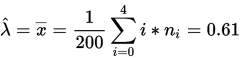
提出假设: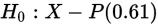 ,若
,若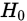 为真时,总体分布律的估计形式为:
为真时,总体分布律的估计形式为:
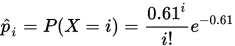
因此,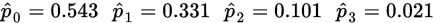
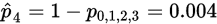 ,其
,其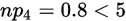 因此将
因此将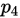 合并到
合并到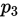 .
. 计算得:
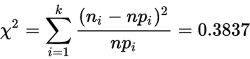
合并后,k=4,r=1,查表知: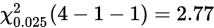 ,即
,即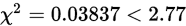 ,不满足拒绝条件,即认为在显著性水平
,不满足拒绝条件,即认为在显著性水平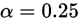 下,样本来自泊松分布。
下,样本来自泊松分布。